베이지안 네트워크 서론
현재 많은 문제(Task)에 대해 딥러닝 기반의 모델들이 훌륭한 성능을 내고 있어 학계와 산업계에서 딥러닝이 큰 각광을 받고 있습니다. 그러나 아직까지 딥러닝 모델은 블랙 박스 모델이라는 평가와 함께 설명력(Interpretability)이 부족하다고 평가되고 있습니다. 쉽게 말해서 모델이 문제는 잘 맞추는데 어떻게 해서 그런 답을 냈는지 사람들이 명확하게 알기 어렵다는 것입니다. 이러한 문제점들을 보완하기 위해서 많은 연구들이 진행되고 있지만 여전히 부족한 부분이 많은 것이 사실입니다.
딥러닝 모델이 많은 발전을 이루기 전에도 예전부터 많은 인공지능 모델이나 기법들이 연구되어 왔습니다. 그 중에서 많은 주목을 받던 모델이 바로 베이지안 네트워크(Bayesian Network)입니다. 베이지안 네트워크는 확률 변수 간의 인과 관계를 그래프 형태로 나타낸 후, 주어진 데이터에 대해 확률 변수의 분포를 학습하는 확률 그래프 모형(Probabilistic Graphical Model, PGM)입니다. 베이지안 네트워크에 대해서 설명하기 앞서 다음의 예제를 살펴보겠습니다.
베이지안 네트워크 예시
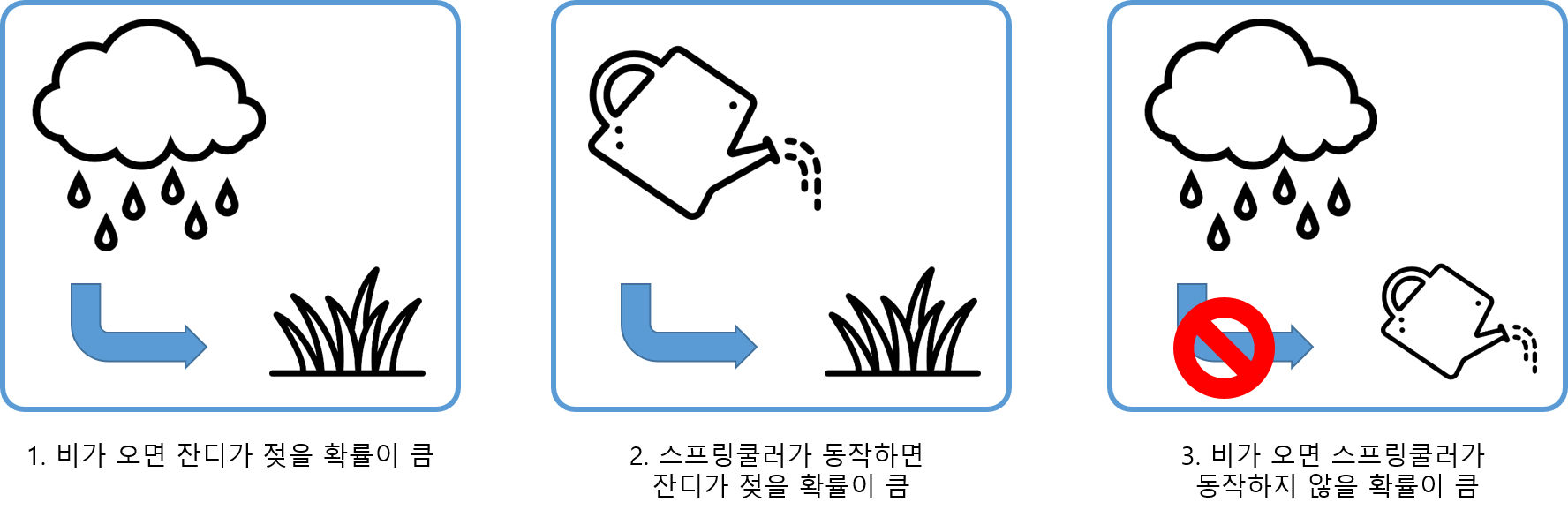
- 비가 오면 잔디가 젖을 확률이 크다.
- 스프링쿨러가 동작하면 잔디가 젖을 확률이 크다.
- 비가 오면 스프링쿨러가 동작하지 않을 확률이 크다.
여러 번의 관측을 통해 각 상황에 대한 확률값을 다음과 같이 얻을 수 있었다고 가정하겠습니다.
- 비가 올 확률
| Rain | Not Rain |
|---|---|
| 0.20 | 0.80 |
- 비에 대한 스프링쿨러가 동작할 확률
| - | On | Off |
|---|---|---|
| Rain | 0.1 | 0.9 |
| Not Rain | 0.5 | 0.5 |
- 비와 스프링쿨러에 대한 잔디가 젖을 확률
| - | Wet | Dry |
|---|---|---|
| Rain + On | 1.0 | 0.0 |
| Rain + Off | 0.6 | 0.4 |
| Not Rain + On | 0.7 | 0.3 |
| Not Rain + Off | 0.1 | 0.9 |
이렇게 주어진 상황에서 베이지안 네트워크를 통해 다음과 같은 질문에 대답할 수 있습니다
만약 잔디가 젖어있다면 비가 왔을 확률은?
베이지안 네트워크 예시 분석
베이지안 네트워크는 확률 변수 간의 인과 관계를 그래프로 나타내어 분석합니다. 일반적으로 그래프는 노드(Node)와 엣지(Edge)로 표현할 수 있습니다. 베이지안 네트워크에서의 노드는 확률 변수가 되고, 엣지는 확률적인 관계가 됩니다. 위의 상황에서는 총 3개의 확률 변수가 존재합니다.
- R : 비가 왔다(Rain, R = 1) / 비가 오지 않았다 (Not Rain, R = 0)
- S : 스프링쿨러가 동작했다 (On, S = 1) / 스프링쿨러가 동작하지 않았다 (Off, S = 0)
- G : 잔디가 젖었다 (Wet, G = 1) / 잔디가 젖지 않았다 (Dry, G = 0)
질문에서 비가 왔는지 여부와 스프링쿨러가 동작했는지는 확인할 수 없고, 잔디가 젖었다는 것만 확인할 수 있으므로 R과 S는 관측 불가능한 변수, 즉 은닉 변수(Hidden variable)이고, G는 관측 가능한 변수, 즉 관측 변수(Observed variable)이 됩니다. 그래프로 나타낼 때에는 은닉 변수는 비어있는 동그라미로, 관측 변수는 색이 칠해진 동그라미로 표시합니다.
또한 다음과 같이 확률 변수 간의 관계가 존재합니다.
- $ P(S = 1 | R = 1) = 0.1 $ : 비에 대한 스프링쿨러가 동작할 확률
- $ P(G = 1 | S = 1, R = 1) = 1.0 $ : 비와 스프링쿨러에 대한 잔디가 젖을 확률
이 관계를 엣지로 표현할 때에는 원인이 되는 변수에서 결과로 나타내지는 변수로 화살표의 형태로 선을 그어 나타내게 됩니다. 따라서 위의 상황을 확률 변수를 노드로 인과관계를 엣지로 표현하면 다음과 같이 표현할 수 있습니다.
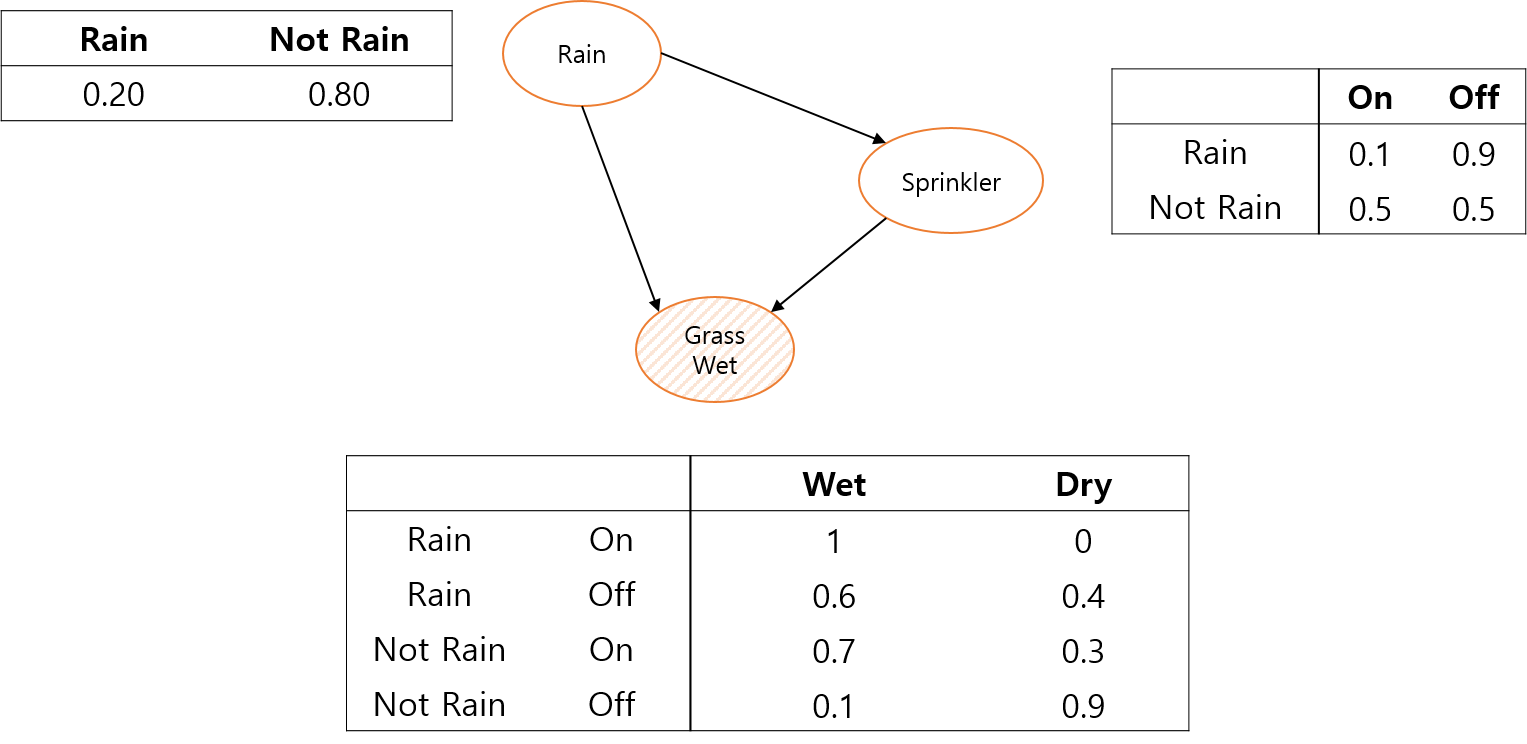
베이지안 네트워크는 인과 관계가 명시되어 있으므로 설명력(Interpretability) 측면에서는 강점을 가지고 있지만, 모델에 포함되는 확률 변수나 그들의 인과 관계가 모두 모델을 설계하는 모델러의 주관이 반영된 것입니다. 따라서 모델러가 어떤 주관을 갖고 어떤 설계를 하는지에 따라 데이터를 설명하는 모델의 성능이 달라질 수 있습니다.
만약 잔디가 젖어있다면 비가 왔을 확률은? 라는 질문에 답하기 위해 먼저 결합 확률 분포(Joint distribution) 을 계산하여야 합니다. 주어진 상황은 서로의 인과 관계에 의해 원인이 조건부가 되는 조건부 확률(Conditional probability)이 되어 다음과 같이 결합 확률 분포를 분해(Decomposition) 할 수 있습니다.
위에서 구한 결합 확률 분포에 의해 다음과 같이 만약 잔디가 젖어있다면 비가 왔을 확률은?에 대한 답은 다음과 같이 계산할 수 있습니다.
베이지안 네트워크는 우리가 관심 있는 확률 변수들 간의 상관 관계 혹은 인과 관계를 그래프로 나타내고, 주어진 데이터를 통해 확률 분포를 계산하여 원하는 질문에 대답을 찾는 모델입니다.
위의 예시와 같은 과정을 통해 베이지안 네트워크라는 주어진 모델과 데이터를 가지고 여러가지 관련된 확률 문제에 대답을 할 수 있습니다. 뿐만 데이터를 설명하거나 데이터에 대한 결론을 찾는 여러가지 문제를 풀 수 있는데, 베이지안 네트워크로 대답할 수 있는 추론 문제는 다음과 같습니다.
베이지안 네트워크의 추론 문제
통계적 추론(Inference)이란 관찰된 표본(데이터)을 바탕으로 모집단에 대한 일반적인 결론을 유도하려는 시도입니다. 우리가 관찰할 수 있는 데이터의 양은 제한되기 때문에 우리는 이 제한된 데이터를 바탕으로 전체의 모집단에 대한 결론을 낼 수 밖에 없습니다. 이러한 결론을 내기 위해서는 확률적인 모형이 필요한데, 우리가 앞에서 다루었던 베이지안 네트워크가 이러한 확률적인 모형 중 하나입니다.
베이지안 네트워크에서는 크게 다음과 같이 3가지 추론 문제를 다루고 있습니다.
- 추론 문제 1 : Likelihood
- 주어진 데이터에 대해 likelihood는 얼마인가?
- 예시. $P(G = 1) = ?$
- 주어진 확률 모델에 따르면 주어진 데이터(G = 1)가 관측될 확률은 얼마인가?
- 추론 문제 2 : Conditional Probability
- 주어진 데이터에 대해 은닉 변수의 조건부 확률은 얼마인가?
- 예시. $P(R = 1 | G = 1) = ?$
- 확률 모델과 데이터가 주어졌을 때 관측되지 않은 은닉 변수가 특정한 값일 확률은 얼마인가?
- 추론 문제 3 : Most Probable Assignment
- 주어진 데이터에 대해 이 데이터를 가장 잘 설명하는 은닉 변수의 값은 얼마인가?
- 예시. $argmax_r P(R = r | G = 1) = ?$
- 확률 모델과 데이터가 주어졌을 때, 주어진 데이터가 관측될 확률이 가장 높기 위해서 은닉 변수의 값은 무엇이 되어야 하는가?
일반적으로 베이지안 네트워크를 이용하여 푸는 문제는 3번째 문제인 경우가 많습니다. 앞에서 살펴본 예제와 같은 경우, 잔디가 젖어있을 때 비가 왔을 확률(추론 문제 2)을 알고 싶기 보다는 비가 왔을지 안 왔을지(추론 문제 3)가 더 중요한 정보가 됩니다. 그러나 3번째 추론 문제를 풀기 위해서는 우선 2번째 추론 문제에 답을 할 수 있어야 하며, 또한 2번째 문제를 풀기 위해서는 1번째 추론 문제에 답을 알아야 합니다. 이렇게 3가지 추론 문제는 서로 연관 관계가 있으며, 가장 중요한 3번째 추론 문제를 풀기 위해서는 위의 3가지 문제에 답을 할 수 있어야 합니다.
결론
베이지안 네트워크는 확률 변수의 인과 관계를 그래프로 나타내고 분석하는 확률 모형입니다. 현재 많은 주목을 받는 딥러닝과 비교했을 때 설명력(Interpretability)에서 강점을 가지지만, 모델러의 주관이 반영된 모델이므로 주관에 따라 모델의 성능이 달라집니다. 베이지안 네트워크를 통해 데이터에 대해 여러가지 추론 문제에 답을 할 수 있습니다.
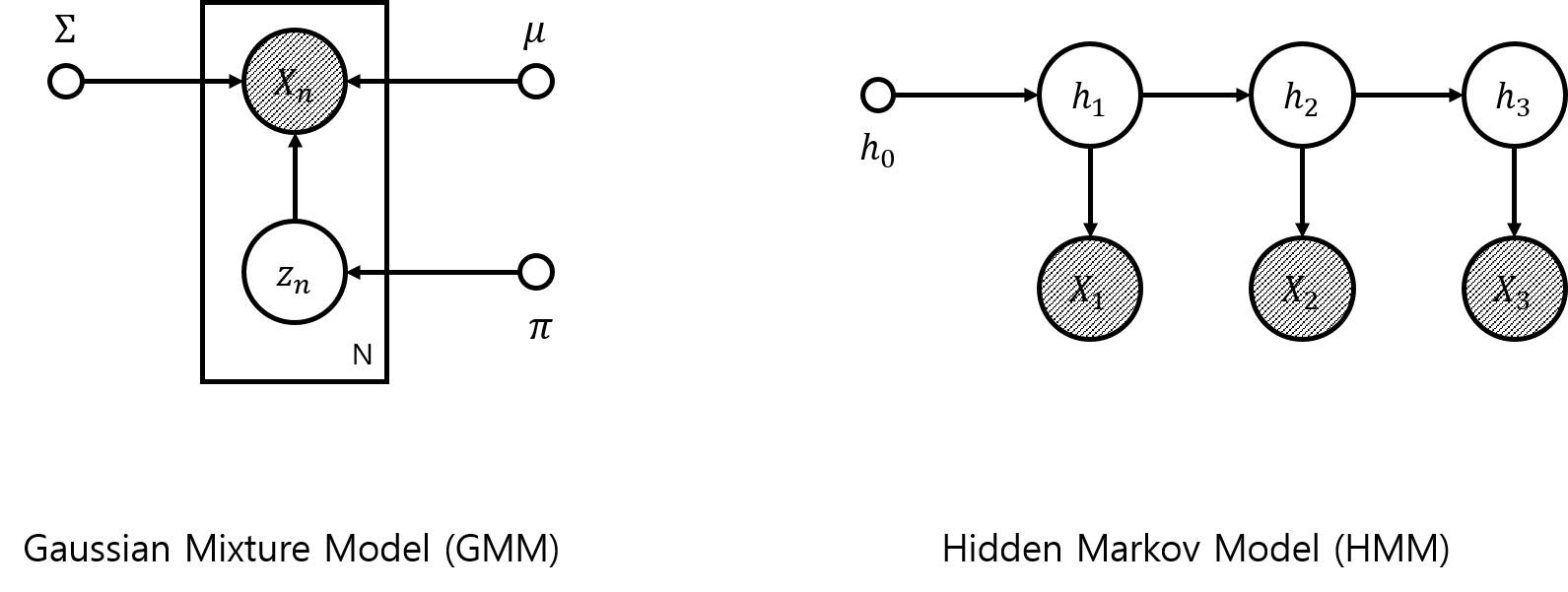
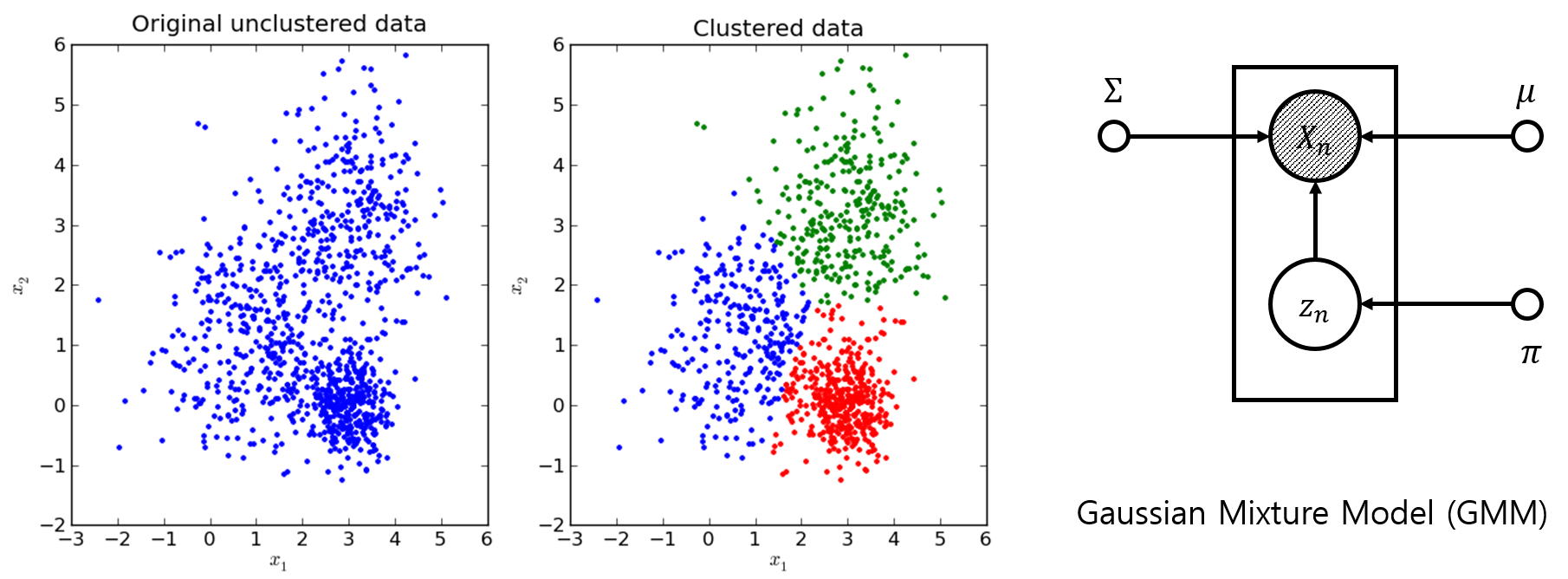
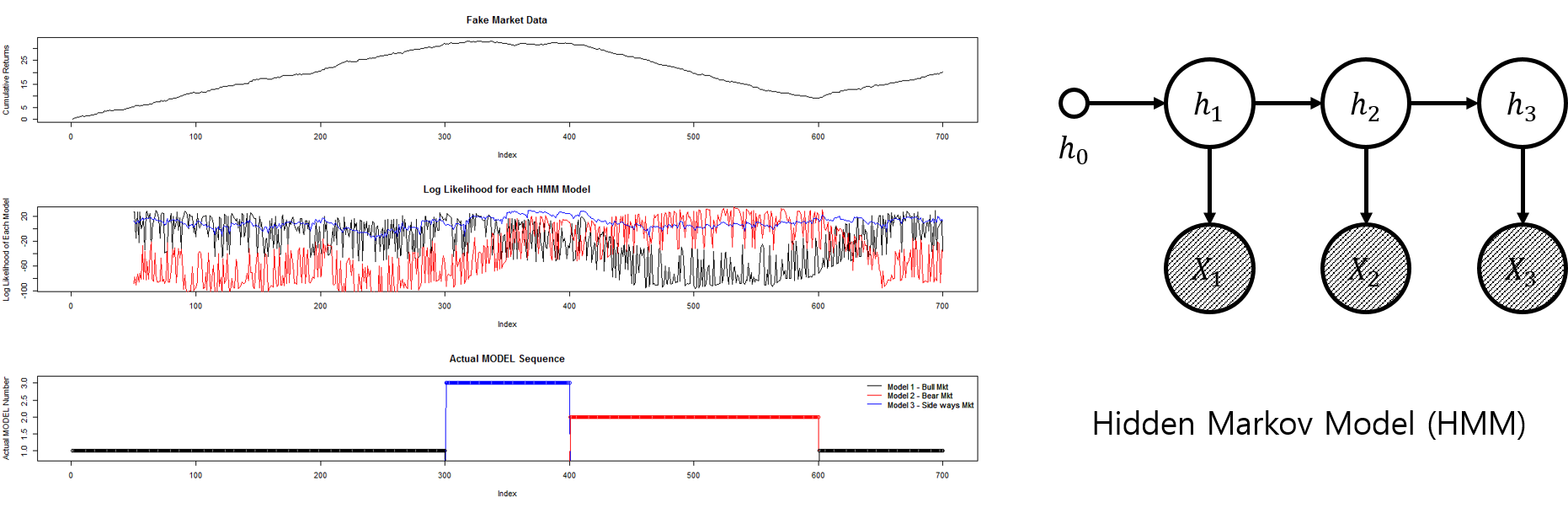
현재까지도 많이 사용되는 모델인 Gaussian Mixture Model (GMM)이나 Hidden Markov Model (HMM)은 모두 베이지안 네트워크의 종류입니다. 다음 글을 통해서 이 두 모델에 대해 각각 알아보겠습니다.